
On average (assuming the rank of the ( k + 1)-st element rank is random), insertion sort will require comparing and shifting half of the previous k elements, meaning that insertion sort will perform about half as many comparisons as selection sort on average.
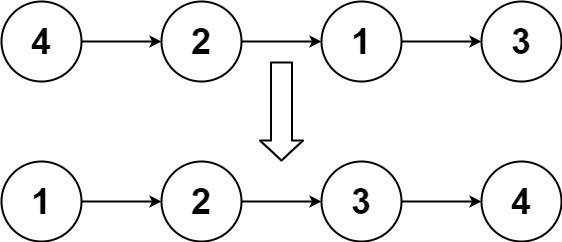
The primary advantage of insertion sort over selection sort is that selection sort must always scan all remaining elements to find the absolute smallest element in the unsorted portion of the list, while insertion sort requires only a single comparison when the ( k + 1)-st element is greater than the k-th element when this is frequently true (such as if the input array is already sorted or partially sorted), insertion sort is distinctly more efficient compared to selection sort. This results in selection sort making the first k elements the k smallest elements of the unsorted input, while in insertion sort they are simply the first k elements of the input. However, the fundamental difference between the two algorithms is that insertion sort scans backwards from the current key, while selection sort scans forwards. As in selection sort, after k passes through the array, the first k elements are in sorted order. Insertion sort is very similar to selection sort. The key that was moved (or left in place because it was the biggest yet considered) in the previous step is marked with an asterisk. In each step, the key under consideration is underlined.


 0 kommentar(er)
0 kommentar(er)
